TLA+: 三个例子
在这篇文章,将会说明如何使用工具来验证伪代码。验证的意思是,可以从伪代码中找 出错误,检查是否符合给定的约束;伪代码的意思是,不是实际的编程语言,意味着它可以 省略掉和解决问题无关的细节。
我们将会以“并发”、“二分查找”和“快速排序”这三个例子来讲解。如果想要实际运行 验证这些伪代码,需要安装 TLA+ Toolbox:从网络上下载 Toolbox 的安装包,解压到一个 目录下就可以了。
下面给出的伪代码是建立在 TLA+ 之上的语言,叫做 PlusCal。这篇文章只是为了引起读者 的兴趣,不会过多地讲解每一步的操作流程。如果你感兴趣,想要动手试验一番,请从网络 上查找资料学习 TLA+ Toolbox 的使用,我推荐从下面的资料开始入手:
并发
在 1965 年,Edsger Dijkstra 发表了一篇经典文章:“Solution of a Problem in Concurrent Programming Control”。在文章中,他提出并解决了一个问题,简略地描述如 下:
有 N 台计算机,它们只能通过读写一个共享存储来进行通信,读和写操作是不可分割
的。每台计算机中有一个进程不停地进行运转,进程中有一个临界区。现在要求为这些
进程编写一个程序,满足以下的条件:
(a) 这些程序都运行同一段代码
(b) 这些进程以任意的速度执行
(c) 进程可以在临界区外的给定执行点停止
(d) 这些进程不会发生活锁
在继续阅读之前,请花几分钟的时间来想想如何解决。只有这样才能感受到这个问题的难度。
通常我们想好了解决方案之后,就是编写代码运行,然后写测试用例看看程序是否运行正常。 这个方法足够好,通常可以应对大部分的情况,但是有一些极端情况是有可能没有考虑到的。 程序员的信心来自于测试用例的覆盖度、问题本身的复杂度、对问题理解的深度。在测试用 例没有覆盖到的情况,是有可能发生错误的。
TLA+ 提供了一种新的思考方式:通过剔除细节,仅用少量的伪代码,来遍历所有的状态空 间,验证是否符合问题的特性。下面将会专注于怎么利用 TLA+ 的工具来验证伪代码,而不 讨论例子中的算法本身,也不讨论 TLA+/PlusCal 的具体语法和语言结构。
能够解决这个问题的方案,需要满足下面的条件:
- 在任何时刻,最多只能有一个进程进入临界区(MutualExclusion)
- 如果有多个进程同时想要进入临界区,它们之中总会有一些可以进入(不会发生活锁)(DeadlockFree)
满足上面的条件,就可以解决上面提出的问题。更进一步,我们还想知道这些进程会不会发 生“饥饿”的情况,不会发生饥饿就需要满足下面的条件
- 任何一个进程,如果想要进入临界区,最终它一定可以进入临界区(StarvationFree)
下面给出的解决方案来自于 Lamport 编写的 TLA+ hyperbook 的第七章 (Mutual Exclusion):
---------------------------- MODULE OneBitMutex ----------------------------
EXTENDS Integers
CONSTANT Procs
ASSUME Procs \subseteq Nat
(***************************************************************************
--algorithm OneBitMutex {
variable x = [i \in Procs |-> FALSE];
fair process (p \in Procs)
variables unchecked = {}, other \in Procs; {
ncs:- while (TRUE) {
e1: x[self] := TRUE;
unchecked := Procs \ {self};
e2: while (unchecked # {}) {
with (i \in unchecked) { other := i; };
unchecked := unchecked \ {other};
e3: if (x[other]) {
if (self > other) {
e4: x[self] := FALSE;
e5: await ~x[other];
goto e1;
} else {
e6: await ~x[other];
}
};
};
cs: skip;
f: x[self] := FALSE;
}
}
}
***************************************************************************)
\* END TRANSLATION
TypeOK == /\ x \in [Procs -> BOOLEAN]
/\ pc \in [Procs -> {"ncs", "e1", "e2", "e3", "e4", "e5", "e6", "cs", "f"}]
Trying(i) == pc[i] \in {"e1", "e2", "e3", "e4", "e5", "e6"}
InCS(i) == pc[i] = "cs"
MutualExclusion == \A i, j \in Procs : (i # j) => ~(InCS(i) /\ InCS(j))
DeadlockFree == (\E i \in Procs : Trying(i)) ~> (\E i \in Procs : InCS(i))
StarvationFree == \A i \in Procs : Trying(i) ~> InCS(i)
=============================================================================
我们使用 TLC 来对上面的代码进行验证,需要首先将 PlusCal 翻译为 TLA+,然后在 TLC 中建立一个模型,将要检查的特性依次填入:MutualExclusion、DeadlockFree、 StarvationFree。通过使用 TLC 进行检查,可以发生上面给出的解决方案不满足饥饿的条 件,检查的结果给出了不满足饥饿条件的运行状态,从初始化到出现问题的整个过程:
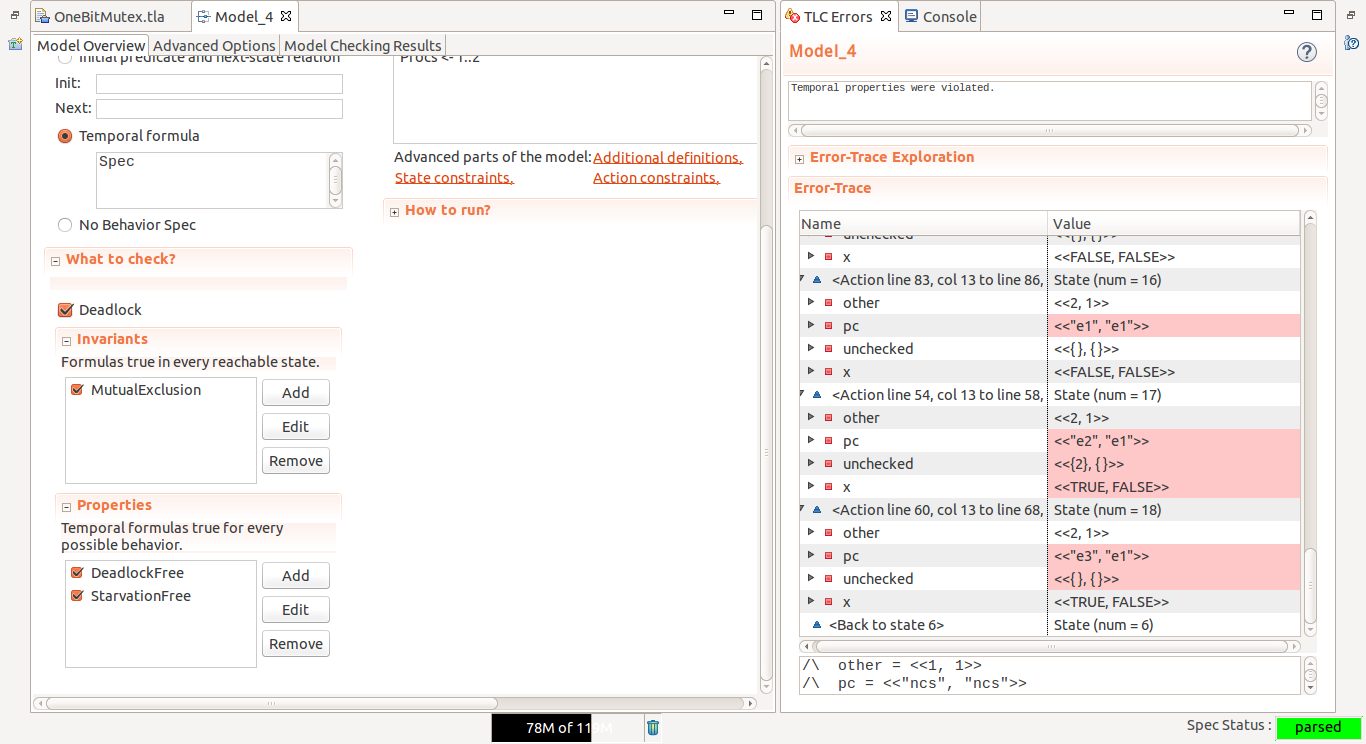
二分查找
二分查找是程序员很熟悉的算法,它需要满足的条件包括:
- 如果需要查找的元素在序列中,最终一定能找到
- 如果需要查找的元素不在序列中,则一定不会找到
下面给出这个算法的伪代码,然后使用 TLC 进行验证:
---------------------------- MODULE BinarySearch ----------------------------
EXTENDS Integers, Sequences, Naturals
CONSTANTS Target
ASSUME Target \in Nat \cup {9}
(***************************************************************************
--algorithm BinarySearch {
variable seqs = {x \in UNION {[1..n -> Nat] : n \in Nat} : \A i,j \in DOMAIN x : (i < j) => x[i] <= x[j]};
fair process (search = 0)
variable testset = seqs \cup {<<1, 2, 3, 3, 3, 4, 4, 5, 5, 9>>}, seq = <<>>, first = 1, mid = 1, last = 1, found = FALSE; {
select:
while (testset # {}) {
seq := CHOOSE x \in testset : TRUE;
testset := testset \ {seq};
first := 1;
last := Len(seq);
mid := first + (last - first) \div 2;
found := FALSE;
sort: while (first <= mid /\ mid <= last) {
if (Target = seq[mid]) {
found := TRUE;
goto select;
} else if (Target < seq[mid]) {
last := mid - 1;
mid := first + (last - first) \div 2;
} else {
first := mid + 1;
mid := first + (last - first) \div 2;
};
};
};
}
}
***************************************************************************)
\* BEGIN TRANSLATION
\* END TRANSLATION
Range(f) == {f[i] : i \in DOMAIN f}
P1 == /\ pc[0] = "sort"
/\ Target \in Range(seq)
/\ found = FALSE
~> found = TRUE
I1 == Target \notin Range(seq) => found = FALSE
Inv == found = FALSE
=============================================================================
下面的结果显示这个算法违反了“对于任何序列,给定的元素都不在序列中”的这个条件, 也就是图中的 Inv 条件。把这个条件删除,再次运行 TLC 就不会看到这个错误了。

快速排序
快速排序需要满足的条件包括:
- 对于给定的序列集合,排序后的每个序列都是有序的
----------------------------- MODULE QuickSort -----------------------------
EXTENDS Sequences, Integers
(***************************************************************************
--algorithm QuickSort {
variables seqs = UNION {[1..n -> Nat] : n \in Nat}, seq = <<>>, result = {};
procedure sort(first = 0, last = 0)
variables lastmin = first, cursor = first + 1, tmp = 0; {
exit:
if (first >= last) {
return;
};
L1:
while (cursor < last) {
if (seq[cursor] <= seq[first]) {
tmp := seq[lastmin];
lastmin := lastmin + 1;
seq[lastmin] := seq[cursor] || seq[cursor] := tmp;
cursor := cursor + 1;
};
};
L2:
call sort(first, lastmin - 1);
L3:
call sort(lastmin + 1, last);
return;
};
{
L4:
while (seqs # {}) {
seq := CHOOSE x \in seqs : TRUE;
seqs := seqs \ {seq};
call sort(1, Len(seq));
L5:
result := result \cup {seq};
};
}
}
***************************************************************************)
\* BEGIN TRANSLATION
\* END TRANSLATION
Sorted(s) == \A i, j \in DOMAIN s : i < j => s[i] <= s[j]
Inv1 == \A x \in result : Sorted(x)
Inv2 == Len(seq) = 0 => first >= last
=============================================================================
我们使用 TLC 进行检查,发现上面给出的算法出现了错误,TLC 给出了错误发生的一系列 状态:
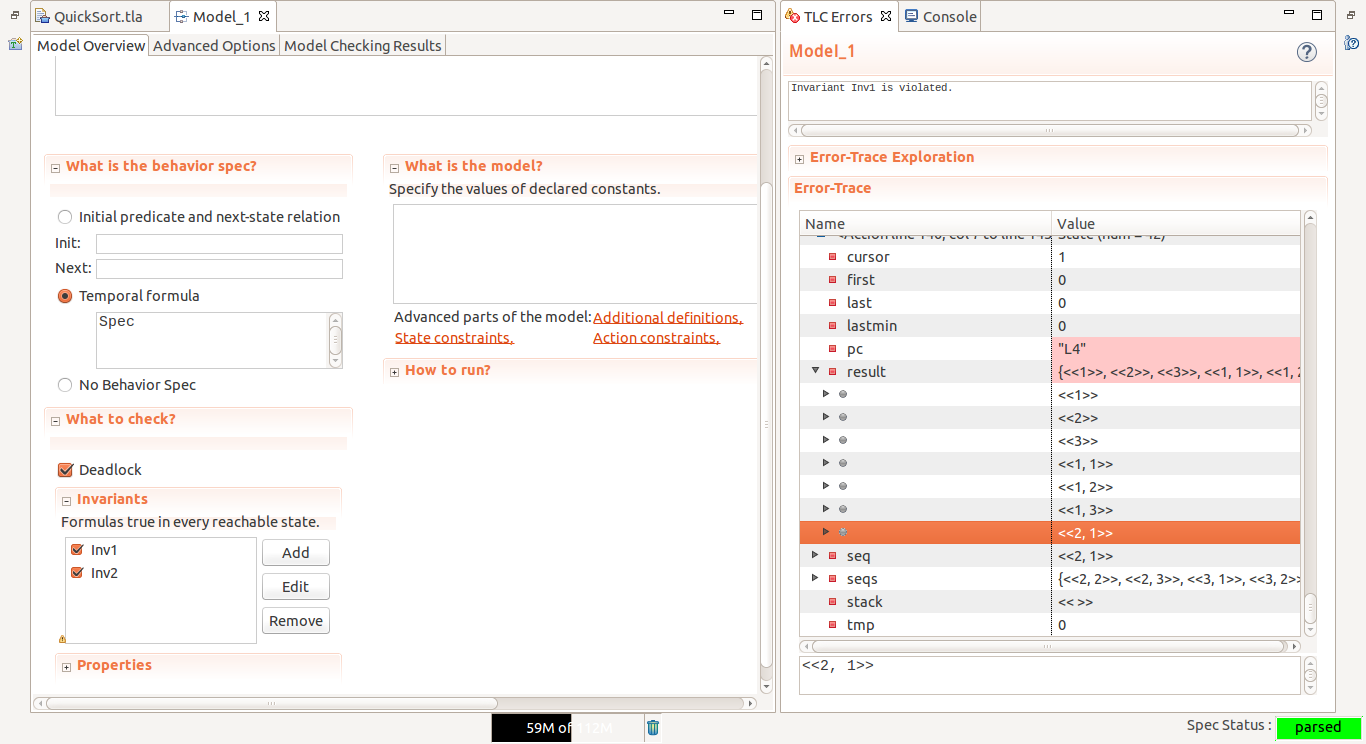
总结
通过上面的例子可以看出,写出 PlusCal 这样的伪代码的行数很少,但是它却有一个工具 可以检查所有的状态空间是否满足某个特性。当然,这样的穷举也会出现不能处理超大的状 态空间,但是足够处理现实中的有限状态了:比如,使用 PlusCal 来编写一个 API 的伪代 码,然后用 TLC 检查,这是完全可行的。
在上面给出的例子中,最多就 30 行伪代码,就可以验证算法的特性。而且,在伪代码中指 定了一定的“测试集”。在快速排序的例子中,给出的测试序列的集合包括空序列、所有一 个元素、两个元素、三个元素的所有序列集合:
{<<>>, <<1>>, ..., <<1, 2>>, ..., <<3, 3, 3>>}
TLC 可以提供一个非常强大的特性是,它可以验证“最终”的这个条件。像上面给出的并发 例子,它表达“一个进程想要进入临界区,它最终一定会进入临界区”的代码是:
\A i \in Procs : Trying(i) ~> InCS(i)
同样类似的情况,用编程语言来检验一个插入队列的操作,如果队列满了,线程被挂起,如 何验证这个被挂起的线程最终一定成功地插入到队列中呢?可以确定的是,要花费的工作量 不是仅仅一行代码就可以完成的。